Limit of a sequence

40 languages

• Article
• Talk

• Read
• Edit
• View history

From Wikipedia, the free encyclopedia

For the general mathematical concept, see Limit (mathematics).

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Limit of a sequence" – news · newspapers · books · scholar · JSTOR (May 2017) (Learn how and when to remove this template message)

The sequence given by the perimeters of regular n-sided polygons that circumscribe the unit circle has a limit equal to the perimeter of the circle, i.e. ${\displaystyle 2��}$. The corresponding sequence for inscribed polygons has the same limit.

n	n sin(1/n)
1	0.841471
2	0.958851
...
10	0.998334
...
100	0.999983

As the positive integer ${\displaystyle �}$ becomes larger and larger, the value ${\displaystyle �\cdot \sin \left(\frac{1}{�}\right)}$ becomes arbitrarily close to ${\displaystyle 1}$. We say that "the limit of the sequence ${\displaystyle �\cdot \sin \left(\frac{1}{�}\right)}$ equals ${\displaystyle 1}$."

In mathematics, the limit of a sequence is the value that the terms of a sequence "tend to", and is often denoted using the ${\displaystyle lim}$ symbol (e.g., ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}}$).^[1] If such a limit exists, the sequence is called convergent.^[2] A sequence that does not converge is said to be divergent.^[3] The limit of a sequence is said to be the fundamental notion on which the whole of mathematical analysis ultimately rests.^[1]

Limits can be defined in any metric or topological space, but are usually first encountered in the real numbers.

History[edit]

The Greek philosopher Zeno of Elea is famous for formulating paradoxes that involve limiting processes.

Leucippus, Democritus, Antiphon, Eudoxus, and Archimedes developed the method of exhaustion, which uses an infinite sequence of approximations to determine an area or a volume. Archimedes succeeded in summing what is now called a geometric series.

Grégoire de Saint-Vincent gave the first definition of limit (terminus) of a geometric series in his work Opus Geometricum (1647): "The terminus of a progression is the end of the series, which none progression can reach, even not if she is continued in infinity, but which she can approach nearer than a given segment."^[4]

Newton dealt with series in his works on Analysis with infinite series (written in 1669, circulated in manuscript, published in 1711), Method of fluxions and infinite series (written in 1671, published in English translation in 1736, Latin original published much later) and Tractatus de Quadratura Curvarum (written in 1693, published in 1704 as an Appendix to his Optiks). In the latter work, Newton considers the binomial expansion of (x + o)ⁿ, which he then linearizes by taking the limit as o tends to 0.

In the 18th century, mathematicians such as Euler succeeded in summing some divergent series by stopping at the right moment; they did not much care whether a limit existed, as long as it could be calculated. At the end of the century, Lagrange in his Théorie des fonctions analytiques (1797) opined that the lack of rigour precluded further development in calculus. Gauss in his etude of hypergeometric series (1813) for the first time rigorously investigated the conditions under which a series converged to a limit.

The modern definition of a limit (for any ε there exists an index N so that ...) was given by Bernard Bolzano (Der binomische Lehrsatz, Prague 1816, which was little noticed at the time), and by Karl Weierstrass in the 1870s.

Real numbers[edit]

The plot of a convergent sequence {a_n} is shown in blue. Here, one can see that the sequence is converging to the limit 0 as n increases.

In the real numbers, a number ${\displaystyle �}$ is the limit of the sequence ${\displaystyle ({�}_{�})}$, if the numbers in the sequence become closer and closer to ${\displaystyle �}$, and not to any other number.

Examples[edit]

See also: List of limits

• If ${\displaystyle {�}_{�}=�}$ for constant c, then ${\displaystyle {�}_{�}\to �}$.^{[proof 1][5]}
• If ${\displaystyle {�}_{�}=\frac{1}{�}}$, then ${\displaystyle {�}_{�}\to 0}$.^{[proof 2][5]}
• If ${\displaystyle {�}_{�}=\frac{1}{�}}$ when ${\displaystyle �}$ is even, and ${\displaystyle {�}_{�}=\frac{1}{{�}^2}}$ when ${\displaystyle �}$ is odd, then ${\displaystyle {�}_{�}\to 0}$. (The fact that  whenever ${\displaystyle �}$ is odd is irrelevant.)
• Given any real number, one may easily construct a sequence that converges to that number by taking decimal approximations. For example, the sequence ${\displaystyle 0.3,0.33,0.333,0.3333,\dots }$ converges to ${\displaystyle 1/3}$. Note that the decimal representation ${\displaystyle 0.3333\dots }$ is the limit of the previous sequence, defined by
  $${\displaystyle \mathrm{0.3333...}:=\underset{�\to \mathrm{\infty }}{lim}\sum _{�=1}^{�}\frac{3}{{10}^{�}}}$$

  
• Finding the limit of a sequence is not always obvious. Two examples are ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{\left(1+\frac{1}{�}\right)}^{�}}$ (the limit of which is the number e) and the Arithmetic–geometric mean. The squeeze theorem is often useful in the establishment of such limits.

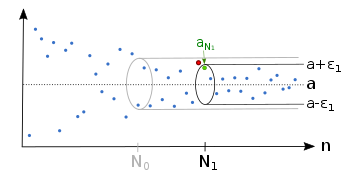
Definition[edit]

We call ${\displaystyle �}$ the limit of the sequence ${\displaystyle ({�}_{�})}$, which is written

${\displaystyle {�}_{�}\to �}$, or

${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}=�}$,

if the following condition holds:

For each real number , there exists a natural number ${\displaystyle �}$ such that, for every natural number ${\displaystyle �\ge �}$, we have .^[6]

In other words, for every measure of closeness ${\displaystyle �}$, the sequence's terms are eventually that close to the limit. The sequence ${\displaystyle ({�}_{�})}$ is said to converge to or tend to the limit ${\displaystyle �}$.

Symbolically, this is:

.

If a sequence ${\displaystyle ({�}_{�})}$ converges to some limit ${\displaystyle �}$, then it is convergent and ${\displaystyle �}$ is the only limit; otherwise ${\displaystyle ({�}_{�})}$ is divergent. A sequence that has zero as its limit is sometimes called a null sequence.

Illustration[edit]

• 

  Example of a sequence which converges to the limit ${\displaystyle �}$.

 
• 

  Regardless which  we have, there is an index ${\displaystyle {�}_0}$, so that the sequence lies afterwards completely in the epsilon tube ${\displaystyle (�-�,�+�)}$.

 
• 

  There is also for a smaller  an index ${\displaystyle {�}_1}$, so that the sequence is afterwards inside the epsilon tube ${\displaystyle (�-{�}_1,�+{�}_1)}$.

 
• 

  For each  there are only finitely many sequence members outside the epsilon tube.

Properties[edit]

Some other important properties of limits of real sequences include the following:

• When it exists, the limit of a sequence is unique.^[5]
• Limits of sequences behave well with respect to the usual arithmetic operations. If ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}}$ and ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}}$ exists, then

${\displaystyle \underset{�\to \mathrm{\infty }}{lim}({�}_{�}\pm {�}_{�})=\underset{�\to \mathrm{\infty }}{lim}{�}_{�}\pm \underset{�\to \mathrm{\infty }}{lim}{�}_{�}}$^[5]

${\displaystyle \underset{�\to \mathrm{\infty }}{lim}�{�}_{�}=�\cdot \underset{�\to \mathrm{\infty }}{lim}{�}_{�}}$^[5]

${\displaystyle \underset{�\to \mathrm{\infty }}{lim}({�}_{�}\cdot {�}_{�})=\left(\underset{�\to \mathrm{\infty }}{lim}{�}_{�}\right)\cdot \left(\underset{�\to \mathrm{\infty }}{lim}{�}_{�}\right)}$^[5]

${\displaystyle \underset{�\to \mathrm{\infty }}{lim}\left(\frac{{�}_{�}}{{�}_{�}}\right)=\frac{\underset{�\to \mathrm{\infty }}{lim}{�}_{�}}{\underset{�\to \mathrm{\infty }}{lim}{�}_{�}}}$ provided ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}\ne 0}$^[5]

${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}^{�}={\left(\underset{�\to \mathrm{\infty }}{lim}{�}_{�}\right)}^{�}}$

• For any continuous function f, if ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}}$ exists, then ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}�\left({�}_{�}\right)}$ exists too. In fact, any real-valued function f is continuous if and only if it preserves the limits of sequences (though this is not necessarily true when using more general notions of continuity).

• If ${\displaystyle {�}_{�}\le {�}_{�}}$ for all ${\displaystyle �}$ greater than some ${\displaystyle �}$, then ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}\le \underset{�\to \mathrm{\infty }}{lim}{�}_{�}}$.
• (Squeeze theorem) If ${\displaystyle {�}_{�}\le {�}_{�}\le {�}_{�}}$ for all ${\displaystyle �}$ greater than some ${\displaystyle �}$, and ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}=\underset{�\to \mathrm{\infty }}{lim}{�}_{�}=�}$, then ${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}=�}$.
• (Monotone convergence theorem) If ${\displaystyle {�}_{�}}$ is bounded and monotonic for all ${\displaystyle �}$ greater than some ${\displaystyle �}$, then it is convergent.
• A sequence is convergent if and only if every subsequence is convergent.
• If every subsequence of a sequence has its own subsequence which converges to the same point, then the original sequence converges to that point.

These properties are extensively used to prove limits, without the need to directly use the cumbersome formal definition. For example, once it is proven that ${\displaystyle 1/�\to 0}$, it becomes easy to show—using the properties above—that ${\displaystyle \frac{�}{�+\frac{�}{�}}\to \frac{�}{�}}$ (assuming that ${\displaystyle �\ne 0}$).

Infinite limits[edit]

A sequence ${\displaystyle ({�}_{�})}$ is said to tend to infinity, written

${\displaystyle {�}_{�}\to \mathrm{\infty }}$, or

${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}=\mathrm{\infty }}$,

if the following holds:

For every real number ${\displaystyle �}$, there is a natural number ${\displaystyle �}$ such that for every natural number ${\displaystyle �\ge �}$, we have ; that is, the sequence terms are eventually larger than any fixed ${\displaystyle �}$.

Symbolically, this is:

.

Similarly, we say a sequence tends to minus infinity, written

${\displaystyle {�}_{�}\to -\mathrm{\infty }}$, or

${\displaystyle \underset{�\to \mathrm{\infty }}{lim}{�}_{�}=-\mathrm{\infty }}$,

if the following holds:

For every real number ${\displaystyle �}$, there is a natural number ${\displaystyle �}$ such that for every natural number ${\displaystyle �\ge �}$, we have ; that is, the sequence terms are eventually smaller than any fixed ${\displaystyle �}$.

Symbolically, this is:

.

If a sequence tends to infinity or minus infinity, then it is divergent. However, a divergent sequence need not tend to plus or minus infinity, and the sequence ${\displaystyle {�}_{�}=(-1{)}^{�}}$ provides one such example.